中２の11月末の「定期テスト」の出題範囲になることが多い【オームの法則】。
【オームの法則】は高校入試でも頻出で、中３の受験勉強においても重要です。
しかし、【オームの法則】が苦手だという中学生はたくさんいます。
公式は覚えていても「直列回路・並列回路・電圧を求める？・電流を求める？・抵抗を求める？」など、質問のパターンが多くて混乱しやすいです。
保護者中学生の子どもが【オームの法則を使う回路の問題】が苦手。
家でなんとかしたいな。
プロ講師エリお任せください！！！
この記事では、【オームの法則を使う回路の問題】を4パターン（公式の確認・直列回路・並列回路・応用）に分けて解説・問題作成しています。
記事を書いた人
この記事の特徴
・答えだけでなく「計算式」を省略せずに記載！
・「例題」で分かる＆「練習問題」で解ける！
・超基礎から応用までを1つの記事に。好きなところにジャンプ！
記事内の問題は無料ダウンロードできます
公式の確認（電圧・電流・抵抗の求め方）
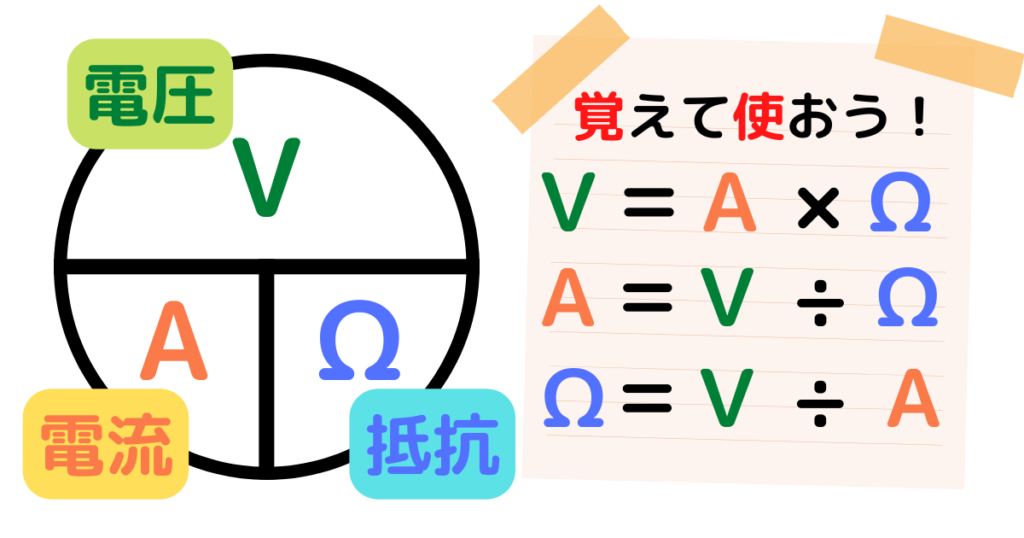
プロ講師エリ電圧・電流・抵抗のうち2つが分かれば、残り1つは計算で求められます！
【オームの法則】とは「抵抗に流れる電流は電圧に比例する」という関係のことです。
この関係から、電圧・電流・抵抗（電気抵抗）をそれぞれ求めることができます。
V（電圧）= A（電流）× Ω（抵抗）
A（電流）= V（電圧）÷ Ω（抵抗）
Ω（抵抗）＝ V（電圧）÷ A（電流）
上の3つの式は、何も見ずに書けるようにしましょう！
練習問題０【かなり易しめ】
- 電圧が 4 V，抵抗が 20 Ω のとき，電流は何 A か。
- 電圧が 8 V，電流が 0.2 A のとき，抵抗は何 Ω か。
- 電流が 0.1 A，抵抗が 50 Ω のとき，電圧は何 V か。
答え（計算式つき）はコチラ
- 0.2 A 4 V ÷ 20 Ω ＝ 0.2 A
- 40 Ω 8 V ÷ 0.2 A ＝ 40 Ω
- 5 V 0.1 A × 50 Ω ＝ 5 V
プロ講師エリ次は「回路図」が登場します。公式の使い方は全く同じです！
練習問題１【易しめ】
以下の回路について、次の問題に答えなさい。
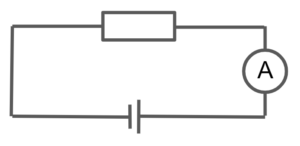
- 電源の電圧は 12 V，抵抗は 30 Ω である。電流計の示す値は何 A か。
- 電源の電圧は 10 V，電流計の示す値は 0.1 A である。抵抗は何 Ω か。
- 電流計の示す値は 0.3 A，抵抗は 60 Ω である。電源の電圧は何 V か。
答え（計算式つき）はコチラ
- 0.4 A 12 V ÷ 30 Ω ＝ 0.4 A
- 100 Ω 10 V ÷ 0.1 A ＝ 100 Ω
- 18 V 0.3 A × 60 Ω ＝ 18 V
直列回路の計算問題
プロ講師エリここからは「例題」で考え方・解き方を徹底解説しています！
例題【直列回路でのオームの法則の使い方】
次のような回路がある。電流計の示す値は 0.2 A，電圧計の示す値は 4 V，抵抗Yは 10 Ω であった。このとき，抵抗Xは何 Ω か。また，電源の電圧は何 V か。
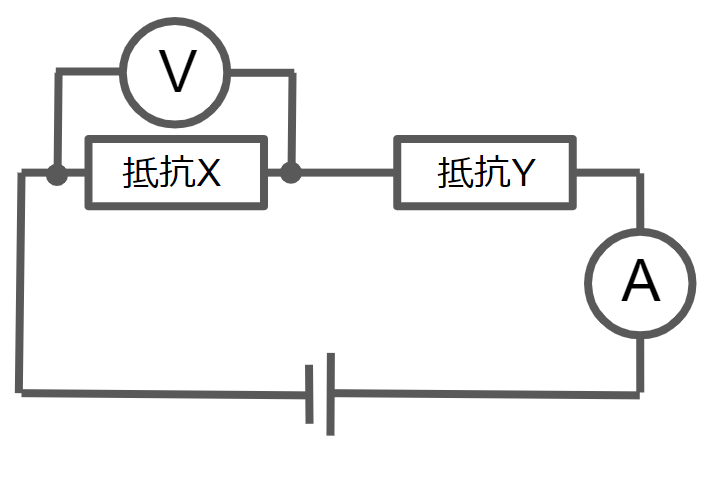
この例題の解き方は大丈夫！すぐに練習問題が解きたい場合はコチラ
プロ講師エリ2つ以上の抵抗がある問題では、
表を書いて埋めていくのがオススメ！
| 抵抗X | 抵抗Y | 全体 | |
| V | 4 | ??? | |
| A | 0.2 | ||
| Ω | ??? | 10 |
他にも数値が入るところがあります。
プロ講師エリ【直列回路に流れる電流はどこでも等しい】ので、
電流は全て 0.2 A です。
| 抵抗X | 抵抗Y | 全体 | |
| V | 4 | ??? | |
| A | 0.2 | 0.2 | 0.2 |
| Ω | ??? | 10 |
上の表の「抵抗X」のように、電圧・電流・抵抗のうち2つが分かれば、残り1つは計算で求められます。
4 V ÷ 0.2 A = 20 Ω
抵抗Xは 20 Ω です。
プロ講師エリ電源の電圧を求めるために、抵抗Yの電圧を計算しましょう！
| 抵抗X | 抵抗Y | 全体 | |
| V | 4 | ??? | |
| A | 0.2 | 0.2 | 0.2 |
| Ω | 20 | 10 |
0.2 A × 10 Ω = 2 V
抵抗Yの電圧は 2 V です。
4 V + 2 V = 6 V
電源の電圧は 6 V です。
プロ講師エリ【直列回路の電源の電圧＝各抵抗の電圧の和】を利用しています！
（電源の電圧を求めるとき、別の解き方もＯＫ！）
【直列回路の全体抵抗＝各抵抗の和】を利用します。
20 Ω + 10 Ω = 30 Ω
0.2 A × 30 Ω = 6 V
電源の電圧は上と同じ 6 V になります。
練習問題２【ふつう】
次のような回路がある。以下の問いに答えなさい。
- 電流計の示す値は 0.1 A，電圧計の示す値は 4 V，抵抗 Y は 10 Ω であった。このとき，抵抗Xは何 Ω か。また，電源の電圧は何 V か。
- 電流計の示す値は 0.1 A，電源の電圧は 10 V，抵抗Xは 60 Ω であった。このとき，抵抗Yは何 Ω か。また，電圧計の示す値は何 V か。
- 電圧計の示す値は 2 V，抵抗Xと抵抗Yはどちらも 20 Ω であった。このとき，電源の電圧は何 V か。また，電流計の示す値は何 A か。
- 電源の電圧は 12 V，抵抗Xは 30 Ω，抵抗Yは 10 Ω であった。このとき，電圧計の示す値は何 V か。また，回路全体の抵抗は何 Ωか。
答えはコチラ
- 抵抗Xは 40 Ω
電源の電圧は 5 V - 抵抗Yは 40 Ω
電圧計の示す値は 6 V - 電源の電圧は 4 V
電流計の示す値は 0.1 A - 電圧計の示す値は 9 V
回路全体の抵抗は 40 Ω
①の表＆計算式はコチラ
| 解き方１ | 抵抗X | 抵抗Y | 全体 |
| V | 4 | 0.1A ×10Ω =1V | 4V +1V =5V |
| A | 0.1 | 0.1 | 0.1 |
| Ω | 4V ×0.1A =40Ω | 10 |
| 解き方２ | 抵抗X | 抵抗Y | 全体 |
| V | 4 | 0.1A ×50Ω =5V | |
| A | 0.1 | 0.1 | 0.1 |
| Ω | 4V ×0.1A =40Ω | 10 | 40Ω +10Ω =50Ω |
②の表＆計算式はコチラ
| 解き方１ | 抵抗X | 抵抗Y | 全体 |
| V | 0.1A ×60Ω =6V | 10V －6V =4V | 10 |
| A | 0.1 | 0.1 | 0.1 |
| Ω | 60 | 4V ÷0.1A =40Ω |
| 解き方２ | 抵抗X | 抵抗Y | 全体 |
| V | 0.1A ×60Ω = 6 V | 10 | |
| A | 0.1 | 0.1 | 0.1 |
| Ω | 60 | 100Ω －60Ω =40Ω | 10V ÷0. 1A =100Ω |
③の表＆計算式はコチラ
| 解き方１ | 抵抗X | 抵抗Y | 全体 |
| V | 2 | 0.1A×20Ω =2V | 2V+2V =4V |
| A | 2V÷20Ω =0.1A | 0.1 | 0.1 A |
| Ω | 20 | 20 |
| 解き方２ | 抵抗X | 抵抗Y | 全体 |
| V | 2 | 0.1A ×40Ω =4V | |
| A | 2V ÷20Ω =0.1A | 0.1 | 0.1 A |
| Ω | 20 | 20 | 20Ω +20Ω =40Ω |
④の表＆計算式はコチラ
| 抵抗X | 抵抗Y | 全体 | |
| V | 0.3A ×30Ω =9V | 12 | |
| A | 0.3 | 0.3 | 12V ÷40Ω =0.3A |
| Ω | 30 | 10 | 30Ω +10Ω =40Ω |
プロ講師エリ「全体抵抗の 40 Ω を求める⇒電流を求める⇒抵抗Xの電圧 9 V を求める」という順番です！
並列回路の計算問題
「直列回路」と「並列回路」の違いに注意！
プロ講師エリ「直列回路」は電流が等しい。「並列回路」は電圧が等しい。
下の表の内容を頭に入れておくことが大切です！
| 直列回路 | 並列回路 | |
|---|---|---|
| Ｖ | 和 （電源の電圧＝各抵抗の電圧の和） | どこでも等しい |
| Ａ | どこでも等しい | 和 （回路全体の電流＝各抵抗に流れる電流の和） |
| Ω | 和 （回路全体の抵抗＝各抵抗の和） | ※ |
※「並列回路」回路全体の抵抗の大きさについて※
並列回路では、回路全体の抵抗は各抵抗よりも小さくなります。
並列回路の回路全体の抵抗＝（各抵抗の積）÷（各抵抗の和）で求めることができますが、応用問題に入るまでは使いません。
例題【並列回路でのオームの法則の使い方】
次のような回路がある。電流計A1の示す値は 0.5 A，電流計A2の示す値は 0.4 A，抵抗Yは 60 Ω であった。このとき，抵抗Xは何 Ω か。また，電源の電圧は何 V か。
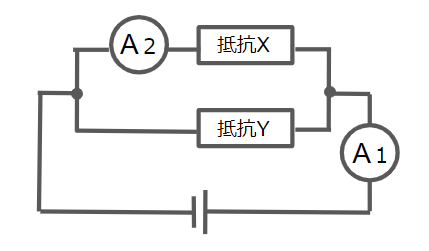
この例題の解き方は大丈夫！すぐに練習問題が解きたい場合はコチラ
プロ講師エリ2つ以上の抵抗がある問題では、表を書いて埋めていくのがオススメ！
| 抵抗X | 抵抗Y | 全体 | |
| V | ??? | ||
| A | 0.4 | 0.5 | |
| Ω | ??? | 60 |
他にも数値が入るところがあります。
プロ講師エリ【並列回路の回路全体の電流は各抵抗に流れる電流の和】を使って、抵抗Yに流れる電流を求めることができます！
| 抵抗X | 抵抗Y | 全体 | |
| V | ??? | ||
| A | 0.4 | 0.5A －0.4A =0.1A | 0.5 |
| Ω | ??? | 60 |
上の表の「抵抗Y」のように、電圧・電流・抵抗のうち2つが分かれば、残り1つは【オームの法則】の計算で求められます。
0.1 A × 60 Ω = 6 V
抵抗Yの電圧は 6 V です。
プロ講師エリ【並列回路の電圧はどこでも等しい】ので、
電圧は全て 6 V です。
| 抵抗X | 抵抗Y | 全体 | |
| V | 6 | 6 | 6 V |
| A | 0.4 | 0.1 | 0.5 |
| Ω | ??? | 60 |
6 V ÷ 0.4 A = 15 Ω
抵抗Xは 15 Ω です。
練習問題３【少し難しめ】
次のような回路がある。以下の問いに答えなさい。
- 電流計A1の示す値は 1.1 A，電流計A2の示す値は 0.5 A，抵抗 Y は 20 Ωであった。このとき，抵抗Xは何 Ω か。また，電源の電圧は何 V か。
- 電源の電圧は 10 V，電流計A2の示す値は 0.5 A，抵抗Yは 20 Ω であった。このとき，電流計A1の示す値は何 A か。また，抵抗Xは何 Ω か。
- 電流計A1の示す値は 0.9 A，電流計A2の示す値は 0.6 A，抵抗Xは 15 Ω であった。このとき，抵抗Yは何 Ω か。また，電源の電圧は何 V か。
- 電源の電圧は 15 V，電流計A1の示す値は 0.4 A，抵抗Yは 50 Ωであった。このとき，電流計A2の示す値は何 A か。また，抵抗Xは何 Ωか。
答えはコチラ
- 抵抗Xは 24 Ω
電源の電圧は 12 V - 電流計A1 の示す値は 1.0 A
抵抗Xは 20 Ω - 抵抗Yは 30 Ω
電源の電圧は 9 V - 電流計A2 の示す値は 0.1 A
抵抗Xは 150 Ω
①の表＆計算式はコチラ
| 抵抗X | 抵抗Y | 全体 | |
| V | 12 | 0.6A ×20Ω = 12 V | 12 V |
| A | 0.5 | 1.1A －0.5A =0.6A | 1.1 |
| Ω | 12V ÷0.5A =24Ω | 20 |
②の表＆計算式はコチラ
| 抵抗X | 抵抗Y | 全体 | |
| V | 10 | 10 | 10 |
| A | 0.5 | 10V ÷20Ω =0.5A | 0.5A +0.5A =1.0A |
| Ω | 10V ÷0.5A =20Ω | 20 |
③の表＆計算式はコチラ
| 抵抗X | 抵抗Y | 全体 | |
| V | 0.6A ×15Ω =9V | 9 | 9 V |
| A | 0.6 | 0.9A －0.6A =0.3A | 0.9 |
| Ω | 15 | 9V ÷0.3A =30Ω |
④の表＆計算式はコチラ
| 抵抗X | 抵抗Y | 全体 | |
| V | 15 | 15 | 15 |
| A | 0.4A －0.3A =0.1A | 15V ÷50Ω =0.3A | 0.4 |
| Ω | 15V ÷0.1A =150Ω | 50 |
プロ講師エリ次はいよいよ応用問題です！
並列回路の計算問題【応用】
並列回路では回路全体の抵抗は各抵抗よりも小さくなります。
並列回路の回路全体の抵抗＝（各抵抗の積）÷（各抵抗の和）で求めることができます。
プロ講師エリ最後の例題＆練習問題です。ここまで分かれば【オームの法則】はもう大丈夫！
例題【並列回路で回路全体の抵抗が必要な応用問題の解き方】
次のような回路がある。電流計A1の示す値は 0.4 A，抵抗Xは 20 Ω，抵抗Yは 60 Ω であった。このとき，電流計A2の示す値は何 A か。また，電源の電圧は何 V か。
例題を飛ばして問題に挑戦したい場合はコチラ
プロ講師エリ2つ以上の抵抗がある問題では、表を書いて埋めていくのがオススメ！
| 抵抗X | 抵抗Y | 全体 | |
| V | ??? | ||
| A | ??? | 0.4 | |
| Ω | 20 | 60 |
20 Ω + 60 Ω = 80 Ω
回路全体の抵抗は 80 Ω ！
これはとてもよくある間違いです。
【回路全体の抵抗が各抵抗の和】になるのは「直列回路」です。
今回は「並列回路」なのでこの考え方はできません。
プロ講師エリ「並列回路」では【回路全体の抵抗＝（各抵抗の積）÷（各抵抗の和）】を使います！
( 20 Ω × 60 Ω ) ÷ ( 20 Ω + 60 Ω ) = 1200 Ω ÷ 80 Ω = 15 Ω
回路全体の抵抗は 15 Ω です。
| 抵抗X | 抵抗Y | 全体 | |
| V | ??? | ||
| A | ??? | 0.4 | |
| Ω | 20 | 60 | 15 |
0.4 A × 15 Ω = 6 V
電源の電圧は 6 V です。
プロ講師エリ【並列回路の電圧はどこでも等しい】ので、
電圧は全て 6 V です。
| 抵抗X | 抵抗Y | 全体 | |
| V | 6 | 6 | 6 V |
| A | ??? | 0.4 | |
| Ω | 20 | 60 | 15 |
6 V ÷ 20 Ω = 0.3 A
電流計A2の値は 0.3 A
プロ講師エリ【回路全体の抵抗】の求め方さえ間違えなければ、これまでの解き方と同じです！
練習問題４【難しめ】
次のような回路がある。電流計A1の示す値は 1.2 A，抵抗Xは 30 Ω，抵抗Yは 10 Ω であった。このとき，電流計A2の示す値は何 A か。また，電源の電圧は何 V か。
答えはコチラ
電流計A1 の示す値は 0.3 A
電源の電圧は 9 V
計算式はコチラ
| 抵抗X | 抵抗Y | 全体 | |
| V | 9 | 9 | 1.2A ×7.5Ω =9V |
| A | 9V ÷30Ω ＝0.3A | 1.2 | |
| Ω | 30 | 10 | (30×10) ÷(30+10) =300÷40 =7.5Ω |
プロ講師エリよく頑張りました！
【オームの法則】まとめ
この記事では、【オームの法則を使う回路の問題】を4パターン（公式の確認・直列回路・並列回路・応用）に分けて解説・問題作成しています。
記事内の問題は無料ダウンロードできます
プロ講師エリ【オームの法則を使う回路の問題】は中２の定期テストでも中３の入試でも重要！！！
子どもたちには「一度解いて終わり」ではなく「復習」して自信をつけてほしいです。
【オームの法則】のポイント
・【オームの法則】とは、「抵抗に流れる電流は電圧に比例する」という関係のこと。
この関係をもとにした3つの式を覚えて使いこなそう！
V（電圧）= A（電流）×Ω（抵抗）
A（電流）= V（電圧）÷Ω（抵抗）
Ω（抵抗）＝ V（電圧）÷ A（電流）
・「2つ以上の抵抗」がある問題では、表を書いて数値を埋めながら問題を解く
【直列回路に流れる電流はどこでも等しい】
【並列回路に流れる電圧はどこでも等しい】
・応用問題を解くとき注意！
【回路全体の抵抗が各抵抗の和】になるのは「直列回路」
「並列回路」では【回路全体の抵抗＝（各抵抗の積）÷（各抵抗の和）】を使う
コメント