保護者中１の子どもが数学で苦戦しているみたい。
家でなんとかしたいな。
プロ講師エリお任せください！
「データの活用」は中１の最後に習う単元です。
公式を覚えて計算を解くというよりデータを整理して情報を読み取る練習が大切です。
この記事では【度数分布表】、【ヒストグラム】、【データと確率】の３つの項目について、語句の意味を確認しながら練習問題を解説していきます！
記事内の問題は無料ダウンロードできます
【度数分布表】の特徴と練習問題
ここで学ぶこと
・例題①【度数分布表】に整理する
・例題②【累積度数】と【範囲】を求める
・例題③【最頻値】【中央値】【平均値】を求める
・例題④【相対度数】と【累積相対度数】を求める
プロ講師エリ気になる例題をタップでジャンプできます！
例題①【度数分布表】に整理する
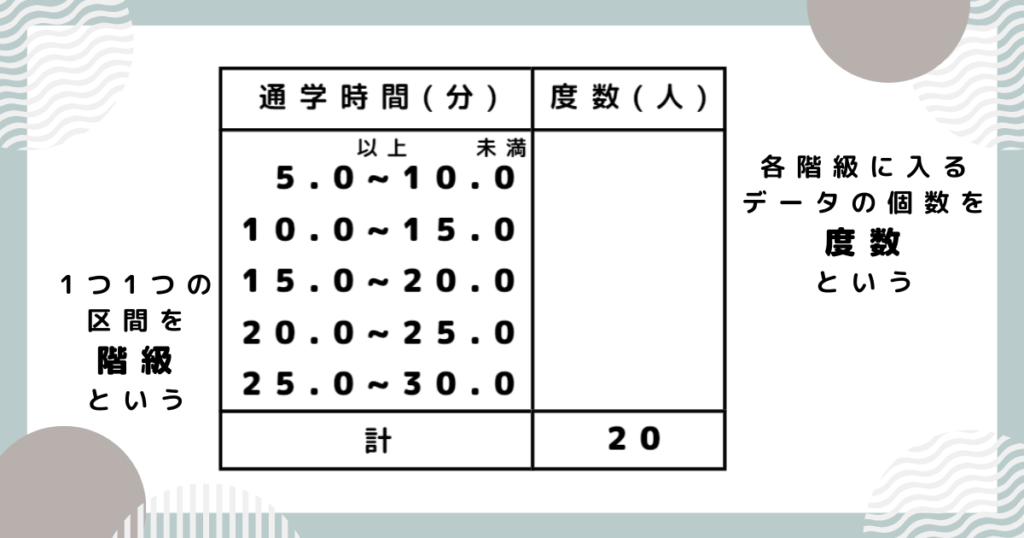
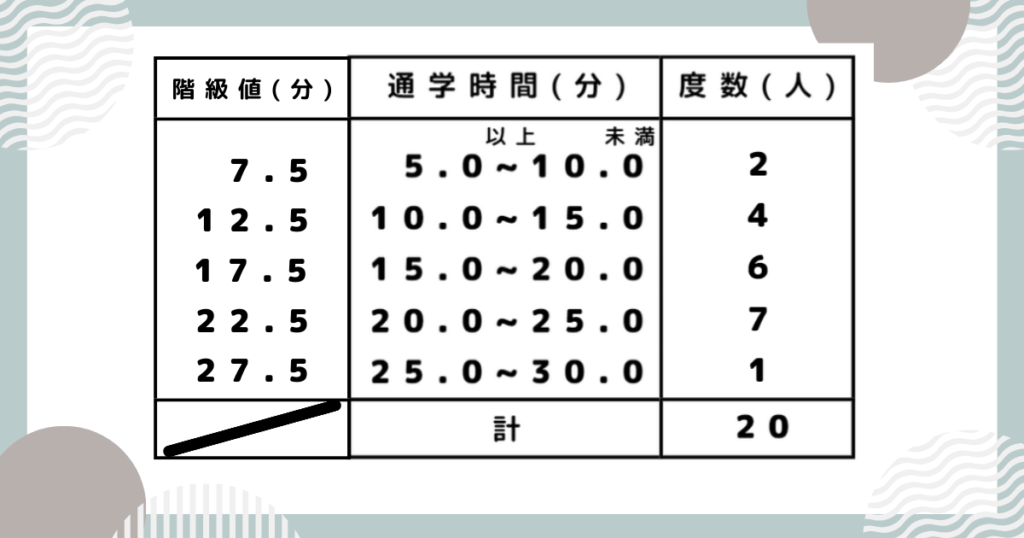
クラス２０人の通学時間を調べました。
度数分布表を用い、このデータを整理していきましょう。
プロ講師エリ以上はその数字を含み、未満は含みません。
１０.０分は一番上ではなく上から二番目の階級となります。
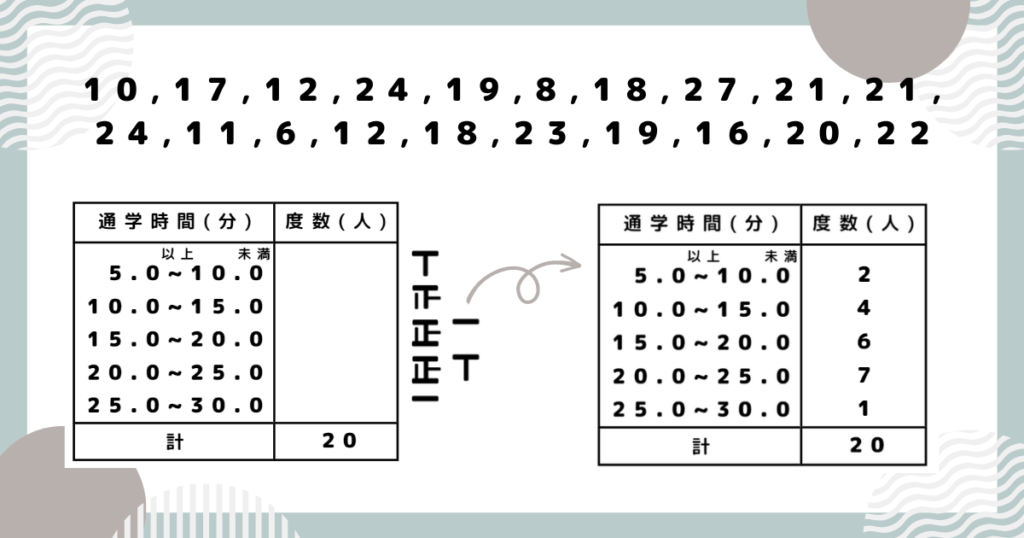
１０,１７,１２・・・と前から順番にどの階級に入るか確認していきます。
「正」の字を書いて数えるとミスが減ります。
また、度数の合計「２＋４＋６＋７＋１」＝「２０」になることを確かめておきましょう。
例題②【累積度数】と【範囲】を求める
累積度数
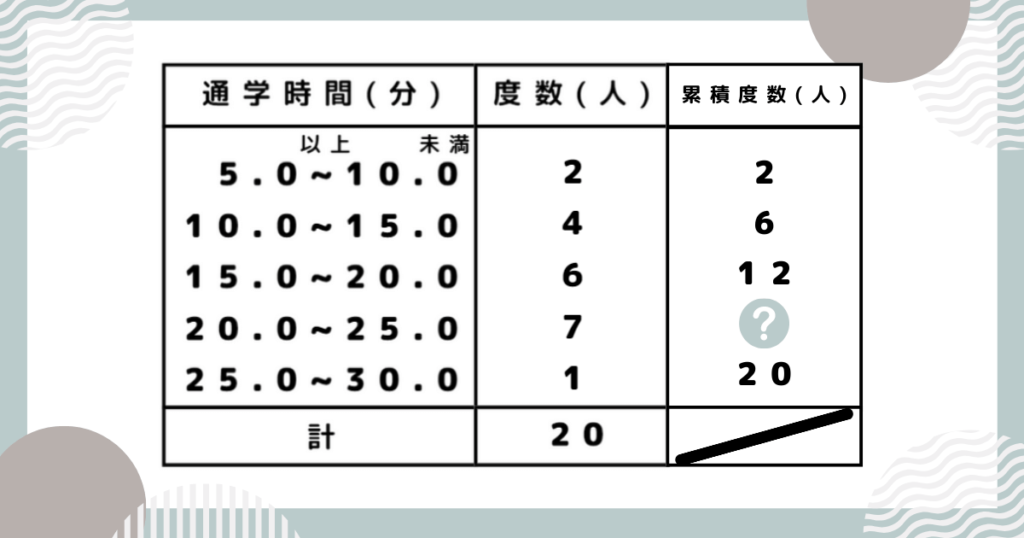
累積度数とは、最初の階級からある階級までの度数の合計のことです。
保護者？の部分に入るのは「１２＋７」＝「１９」だね！
範囲
分布の範囲とは、データの最大値と最小値の差のことです。
保護者範囲は「２７ー６」＝「２１」分ね！
プロ講師エリ単位を忘れずに！！
例題③【最頻値】と【中央値】と【平均値】
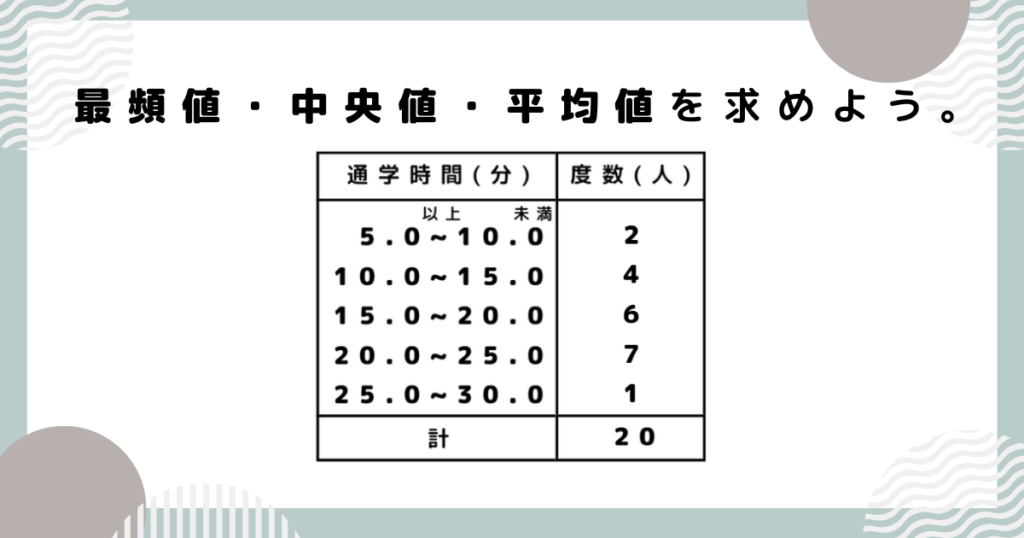
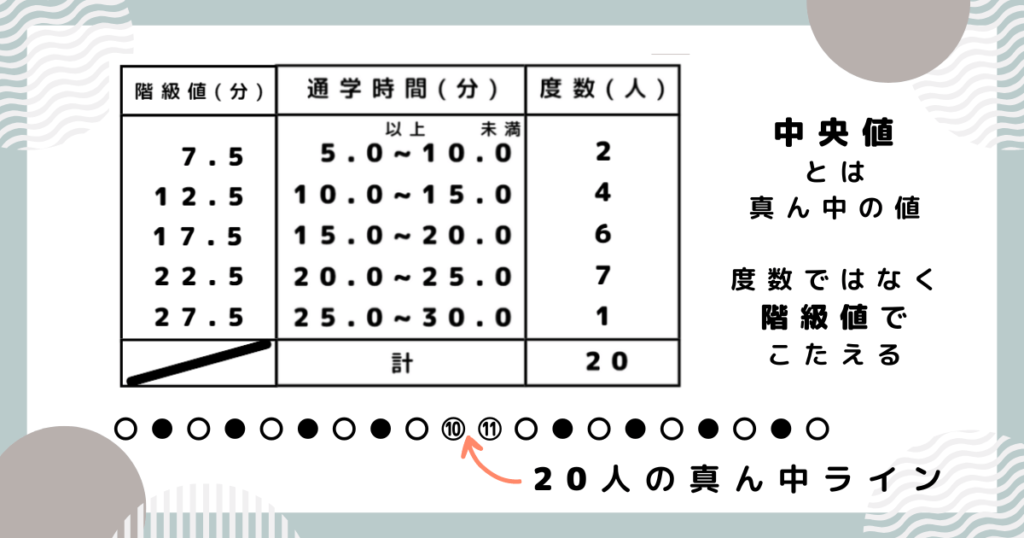
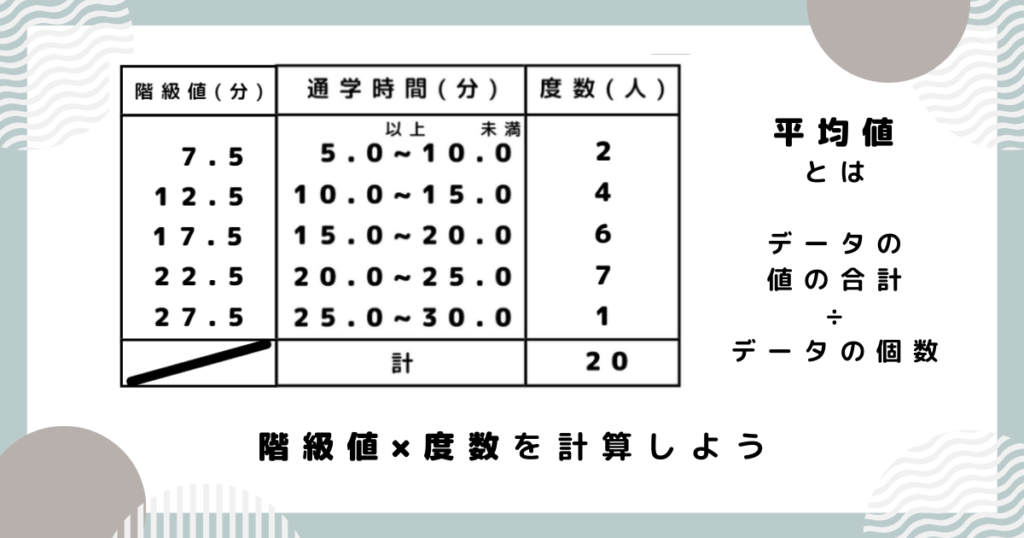
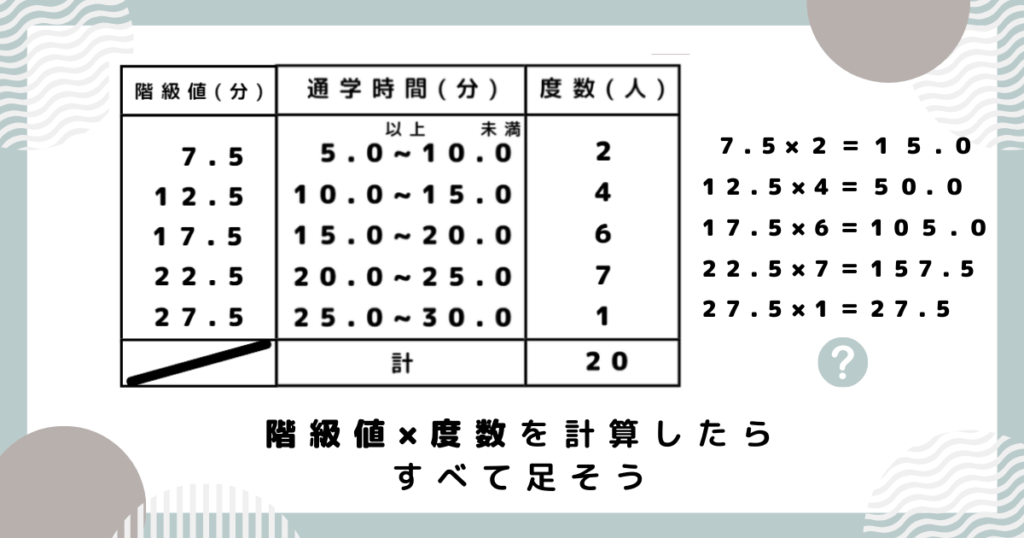
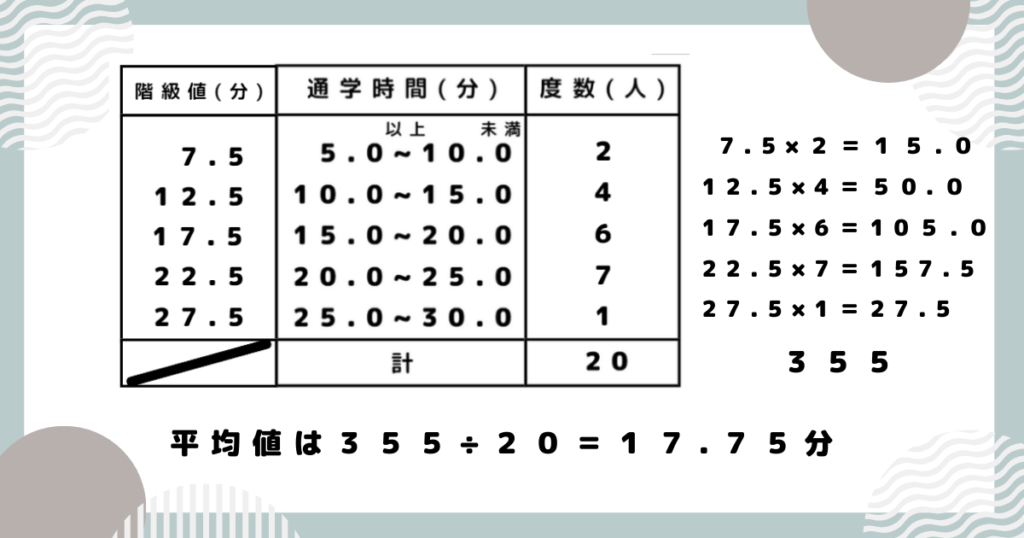
完成した度数分布表をもとに、最頻値・中央値・平均値をそれぞれ求めましょう。
＼ タップで解き方がわかる！／
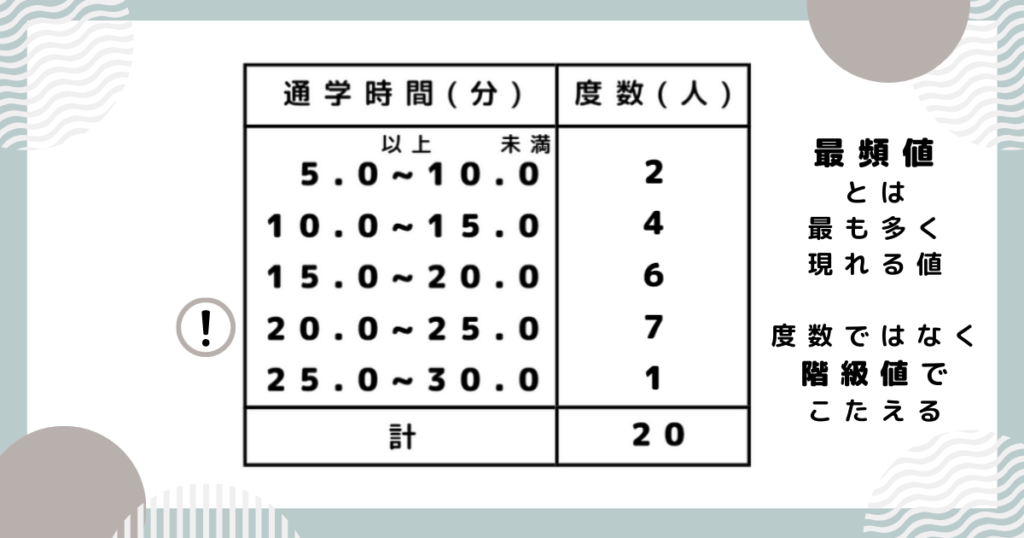
階級値とは、それぞれの階級の真ん中の値のことです。度数分布表でよく用いられます。
保護者単位を忘れずに書いてね！！
例題④【相対度数】と【累積相対度数】を求める
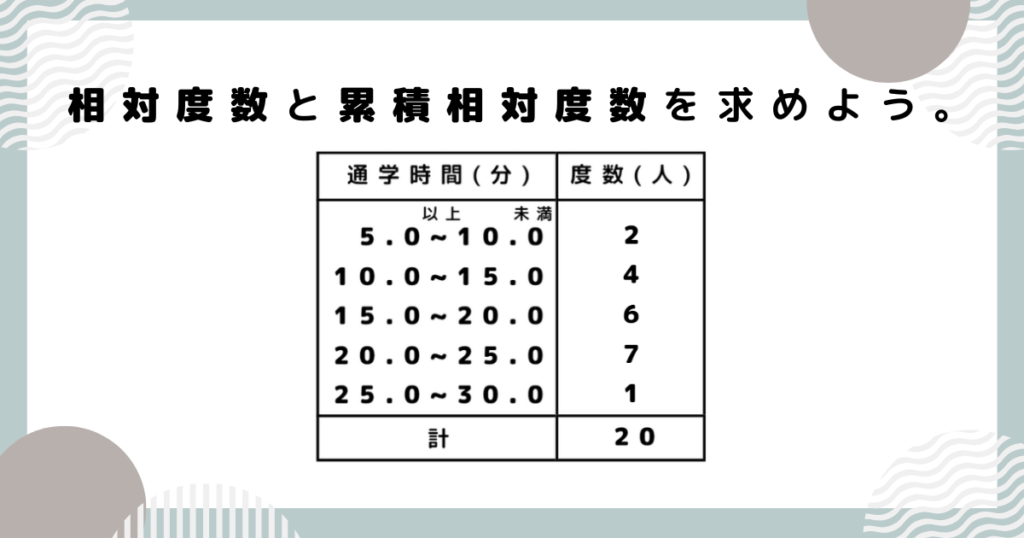
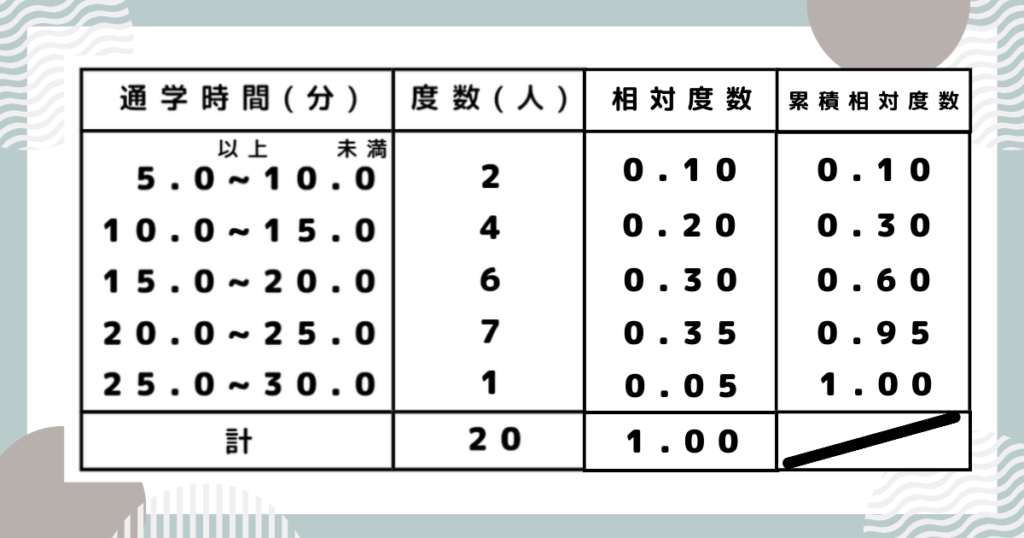
完成した度数分布表をもとに、相対度数・累積相対度数を求めましょう。
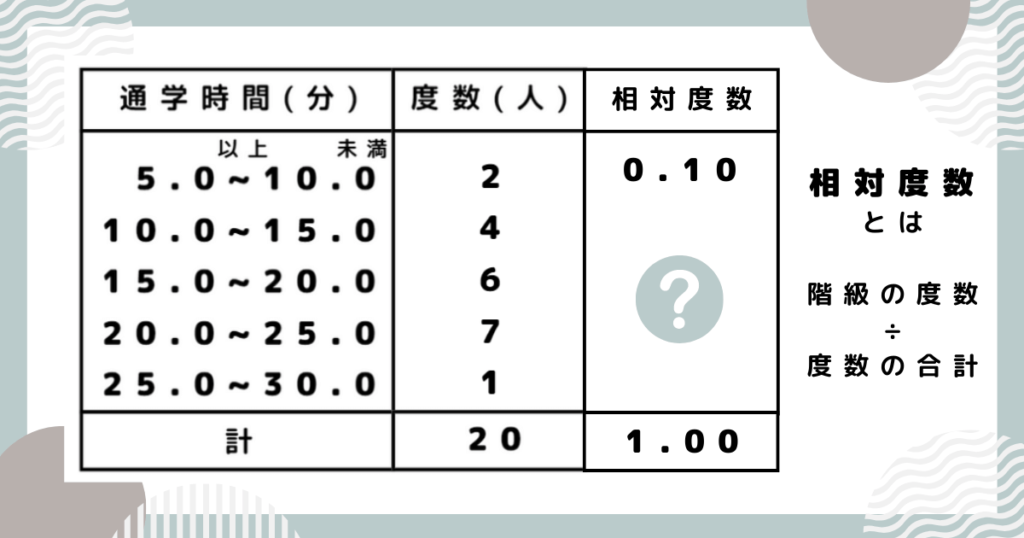
相対度数とは、それぞれの度数の全体に対する割合のことです。
保護者一番上の階級の相対度数は「２÷２０」＝「０.１０」だね！
プロ講師エリ？の部分も、計算して求めましょう。
ここをタップで答え合わせ！
上から二番目 ４÷２０＝０.２０
上から三番目 ６÷２０＝０.３０
上から四番目 ７÷２０＝０.３５
一番下 １÷２０＝０.０５
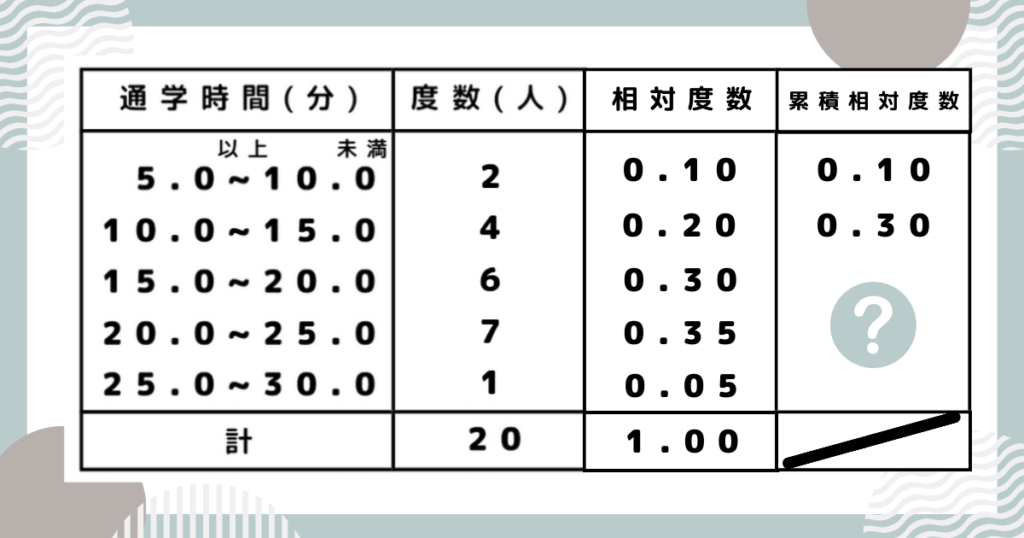
累積相対度数とは、最初の階級からある階級までの相対度数の合計のことです。
保護者上から二番目の階級の累積相対度数は「０.１０＋０.２０」＝「０.３０」！
プロ講師エリ？の部分も、計算して求めましょう。
ここをタップで答え合わせ！
上から三番目 ０.３０＋０.３０＝０.６０
上から四番目 ０.６０＋０.３５＝０.９５
一番下 ０.９５＋０.０５＝１.００
プロ講師エリ相対度数、累積相対度数ともに合計すると「１.００」＝「１００％」になることを覚えておきましょう！
【ヒストグラム】の特徴と練習問題
ギリシャ語で「イストス（直立する）」＋「グラム（記録）」という意味のヒストグラム。
ヒストグラムは別名「柱状グラフ」といいます。
ここで学ぶこと
・例題①【度数分布表】から【ヒストグラム】をかく
・例題②【度数分布多角形】をかく
・例題③【ヒストグラム】の読みとり
・コラム：【ヒストグラム】と【棒グラフ】の違い
プロ講師エリ気になる例題をクリックでジャンプ可能です！
例題①【度数分布表】から【ヒストグラム】をかく
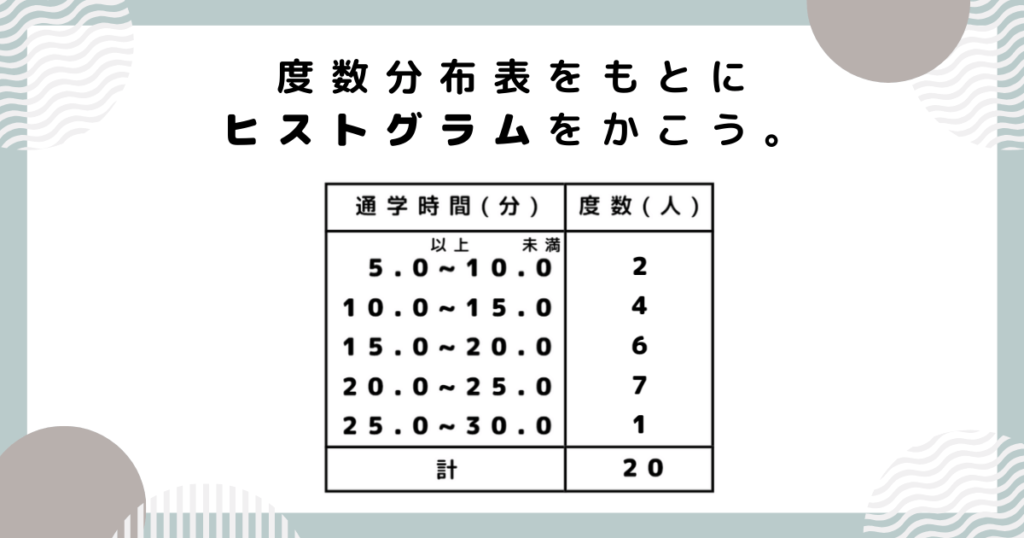
完成した度数分布表をもとに、ヒストグラム（柱状グラフ）をかきましょう。
ここをタップで答え合わせ！
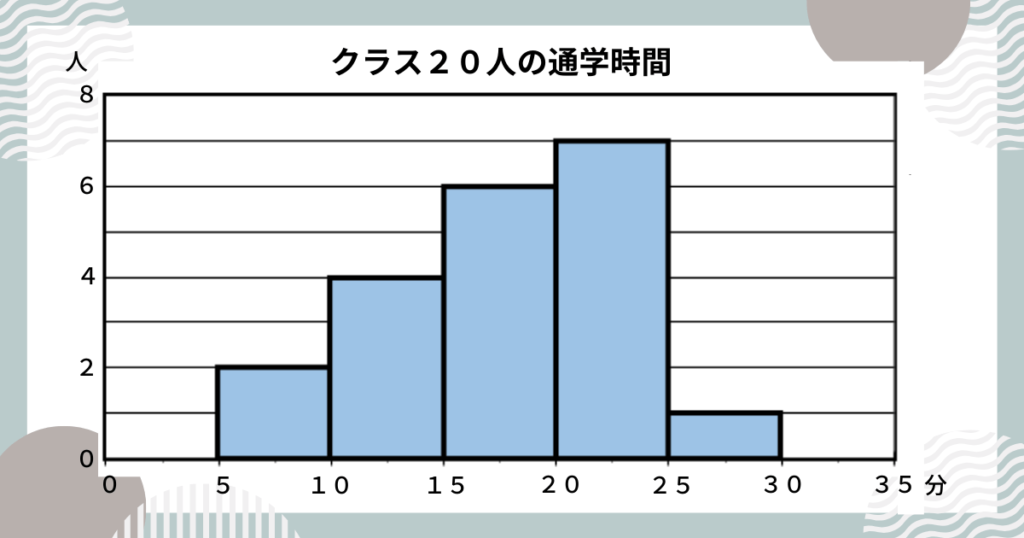
ヒストグラムの柱の部分は、今回のように色で塗りつぶしたり、斜線を引いたりすることがあります。
（見やすくするための工夫です）
誰が見てもわかるように、まっすぐ濃い線でかきましょう。
例題②【度数分布多角形】をかく
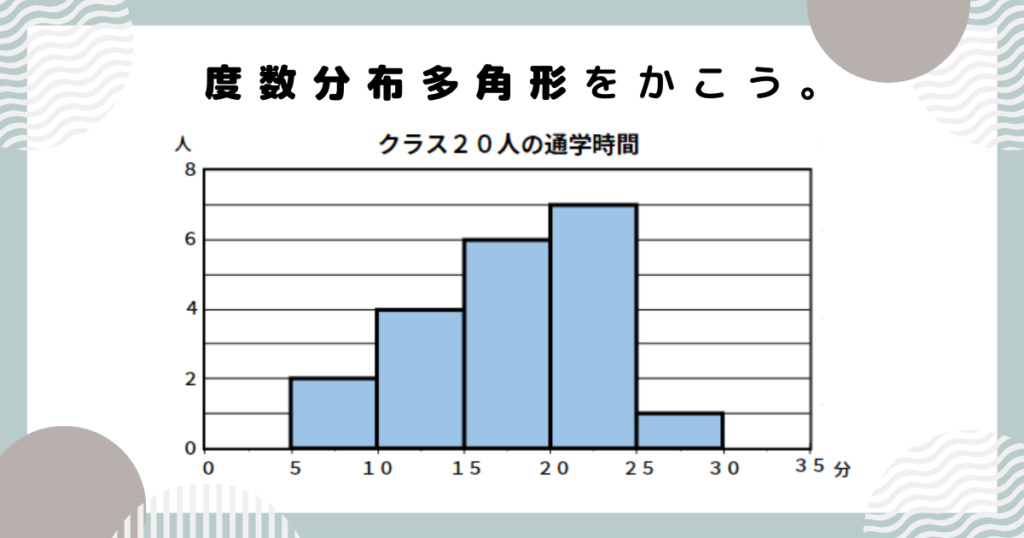
ヒストグラムをもとに、度数分布多角形をかきましょう。
度数分布多角形は別名「度数折れ線」といいます。
プロ講師エリ名前は難しそうですが、カンタンにかけますよ！
ここをタップで答え合わせ！
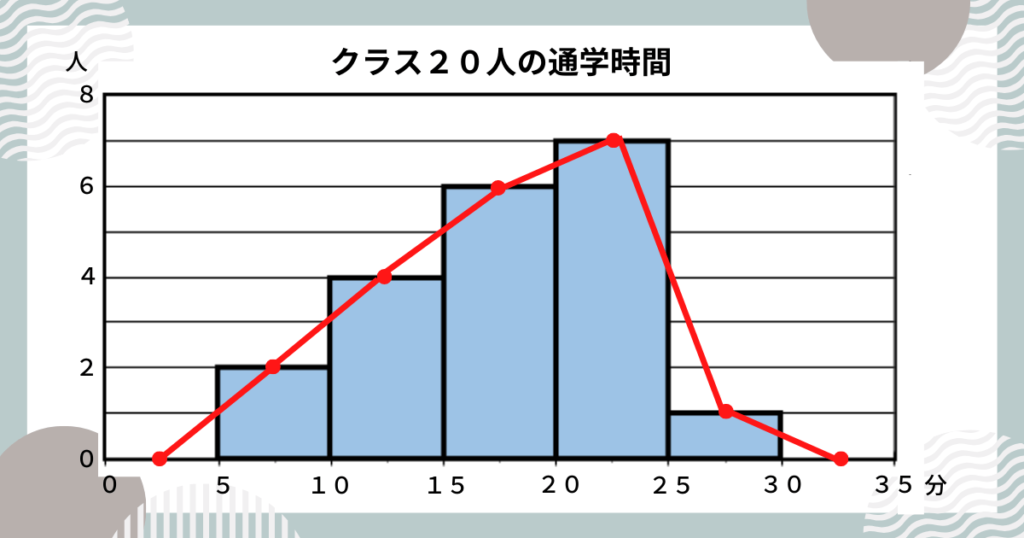
ヒストグラムの柱の、上の辺の「中点」を線分で結びましょう。
両端（今回の場合は０以上５未満、３０以上３５未満）に柱はありませんが、度数が０と考えて「中点」をとります。
定規を使ってかきましょう。
例題③【ヒストグラム】の読みとり
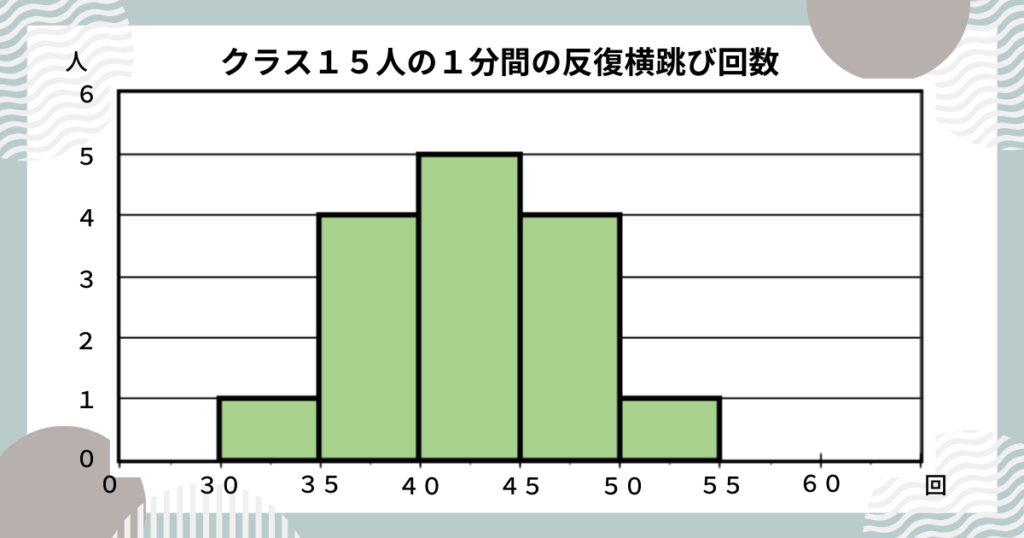
ヒストグラムの読みとりに関する問題を４問出題します。
（タップで答えを確認できます）
（１）階級の幅を答えなさい。
答えは５回
（２）中央値を答えなさい。
答えは４２.５回
プロ講師エリ１５人の真ん中は「８番目」！８番目は、４０回以上４５回未満の階級に含まれています。
保護者４０回以上４５回未満の階級の「階級値」は「４２.５回」ね！
（３）平均値を答えなさい。
答えは４２.５回
保護者「平均値」＝（階級値×度数）の合計÷（データの個数）を計算！！
計算式は
（３２.５×１＋３７.５×４＋４２.５×５＋４７.５×４＋５２.５×１）÷１５
（３２.５＋１５０＋２１２.５＋１９０＋５２.５）÷１５
６３７.５÷１５＝４２.５
（４）最頻値を答えなさい。
答えは４２.５回
プロ講師エリ「最頻値」とは、度数が最も多い「５人」の階級値です！
コラム：【ヒストグラム】と【棒グラフ】の違い
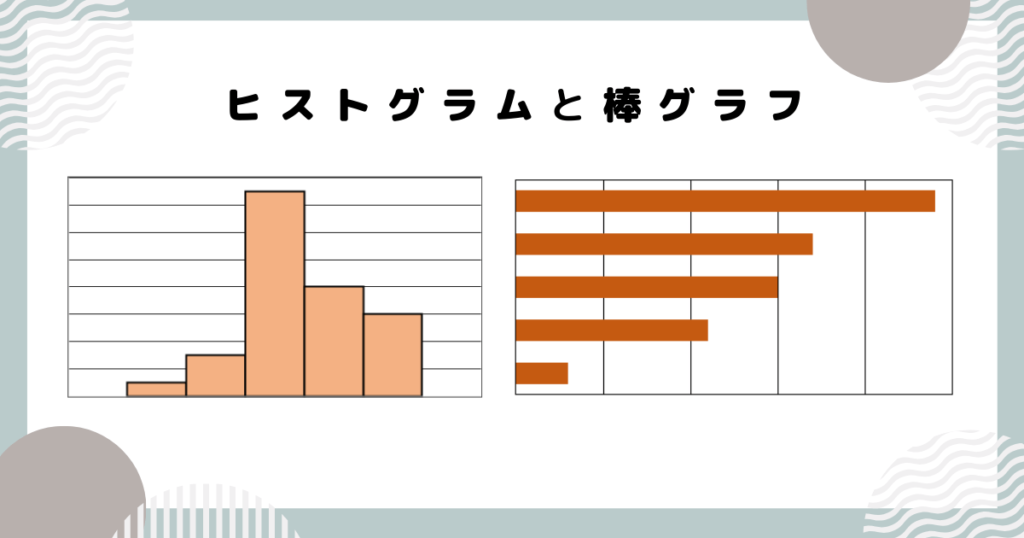
ヒストグラムは別名「柱状グラフ」といいます。
「柱」と「棒」グラフではどのような違いがあるか、同じデータをもとにして比べます。
＼ タップで違いがわかる！／
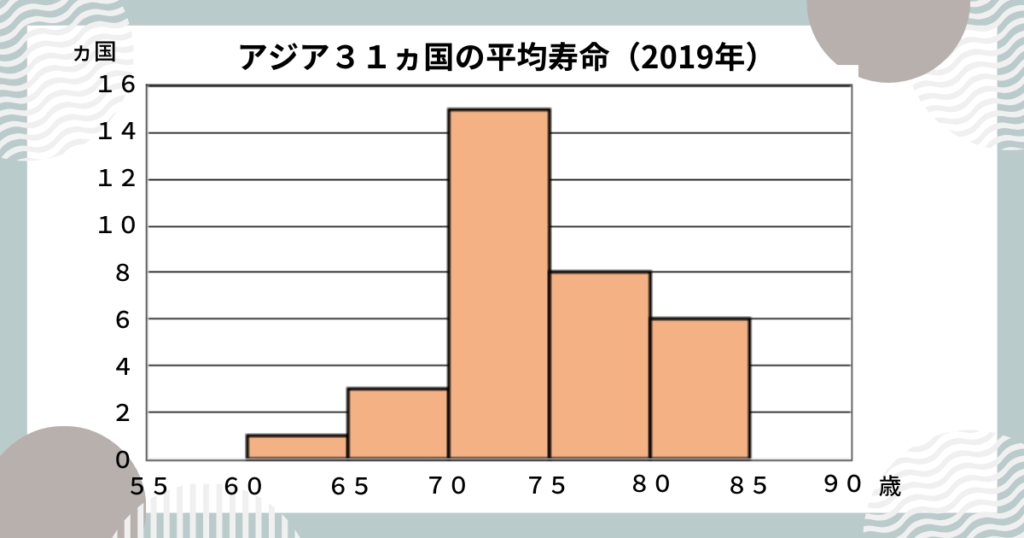
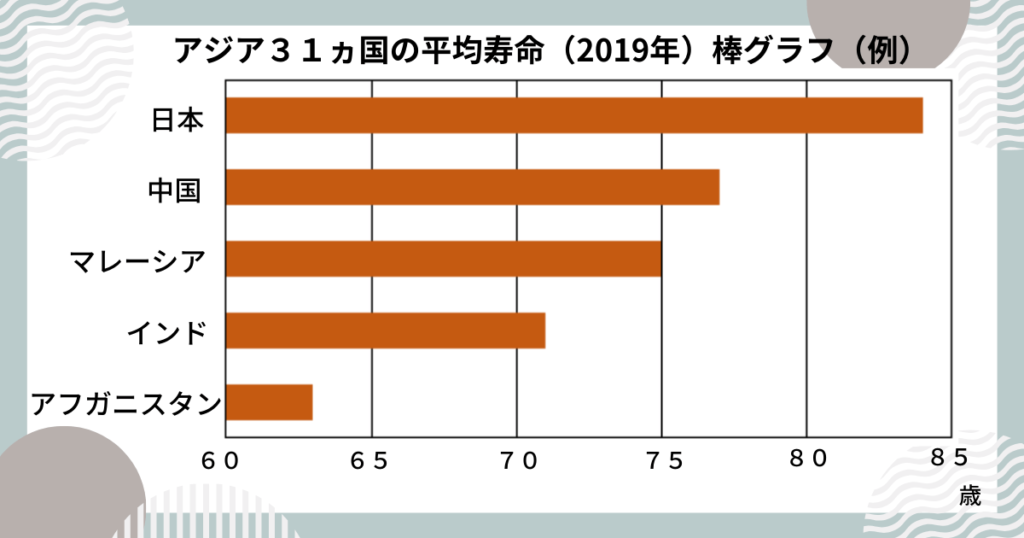
平均寿命が６０歳以上６５歳未満の国が１ヵ国、６５歳以上７０歳未満の国が３ヵ国・・・とカウントして、ヒストグラムを作成しました。
ヒストグラムはアジア３１ヵ国の平均寿命「全体の分布のようす」がわかります！
柱と柱の間に隙間は作りません。（柱一つ一つが独立しているのではなく、すべての柱で度数分布をとらえます）
プロ講師エリ中学生の数学で出てくるのは主に「ヒストグラム」です！
【データと確率】の特徴と練習問題
保護者「確率」って中２で習うんじゃないの？
プロ講師エリ「確率」のメインは中２で習います。
中１の「データと確率」はデータから物事の傾向をつかむという意味合いです。
中１の「データと確率」は2021年の教科書改訂で新しく追加された内容で、保護者世代は習っていません。
「データから物事の傾向をつかむ」とはどのするのか、例題を２つ紹介します。
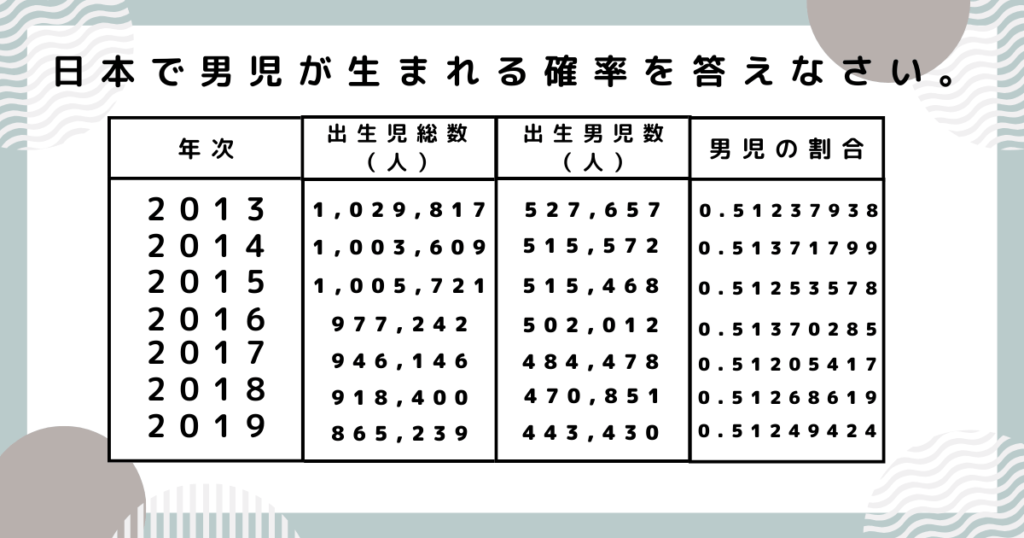
例題①
プロ講師エリ各年次の「男子の割合」は、「出生男児数」÷「出生児総数」で求めています！
２０１３年から２０１９年の７年間では、出生男児数の出生児総数に対する割合はすべて「０.５１」であることがわかります。
長い期間で変わらないので、日本で男児が生まれる確率は「０.５１」と考えられます。
日本で女児が生まれる確率も考えてみましょう。
答えはここをタップ
答えは０.４９
保護者「１.００」ー「０.５１」＝「０.４９」ね！
例題②
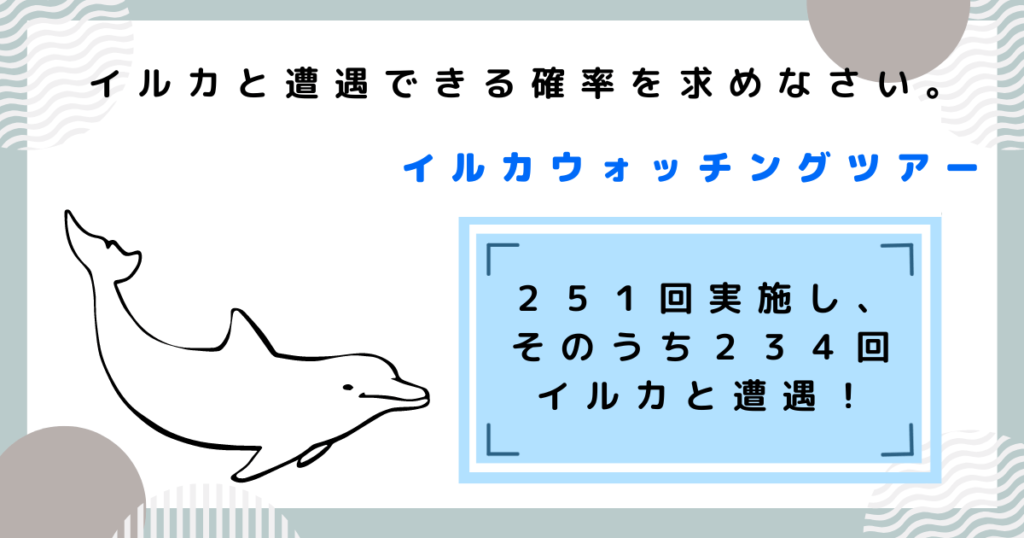
イルカと遭遇できる確率を小数第３位までで答えましょう！
答えはここをタップ！
答えは０.９３２
プロ講師エリ「小数第３位まで」の時は「小数第４位」を四捨五入します。
「２３４」÷「２５１」＝０９３２２・・・・よって、答えは「０.９３２」です。
確率とは、あることがらの起こりやすさの程度のことです。
「あることがらが起こった回数」÷「合計回数」で計算します。
（ことがらの数が多い場合には、相対度数を確率と考えます。答えは分数ではなく小数でかきます）
「中１データの活用」まとめ
この記事では、【度数分布表】、【ヒストグラム】、【データと確率】の３つの項目について、語句の意味を確認しながら練習問題を解説しました。
記事内の問題は無料ダウンロードできます
プロ講師エリ「データの活用」は中２の最後にまた習います！
