プロ講師エリ
プロ講師エリ中2数学「データの活用」の単元は、2021年の教科書改訂で新しく追加されました。「資料から情報を読み取る力」が求められます。
 保護者
保護者「資料の読み取り」ができるか心配です。
 プロ講師エリ
プロ講師エリ「四分位数」と「箱ひげ図」がわかっていれば大丈夫です。
不安があれば復習しておきましょう!
\ 復習したい人はクリック! /
\ 復習したい人はクリック! /
この記事を書いた人

この記事で学ぶこと
・「箱ひげ図」の情報が「正しい」か「正しくない」か「わからない」かを選ぶ
⇒例題にジャンプ!
・対応する「箱ひげ図」と「ヒストグラム」を選ぶ
⇒例題にジャンプ!
・「箱ひげ図」を比較して記述する
⇒例題にジャンプ!
記事内の問題は無料ダウンロードできます
例題① 「箱ひげ図」の読み取り
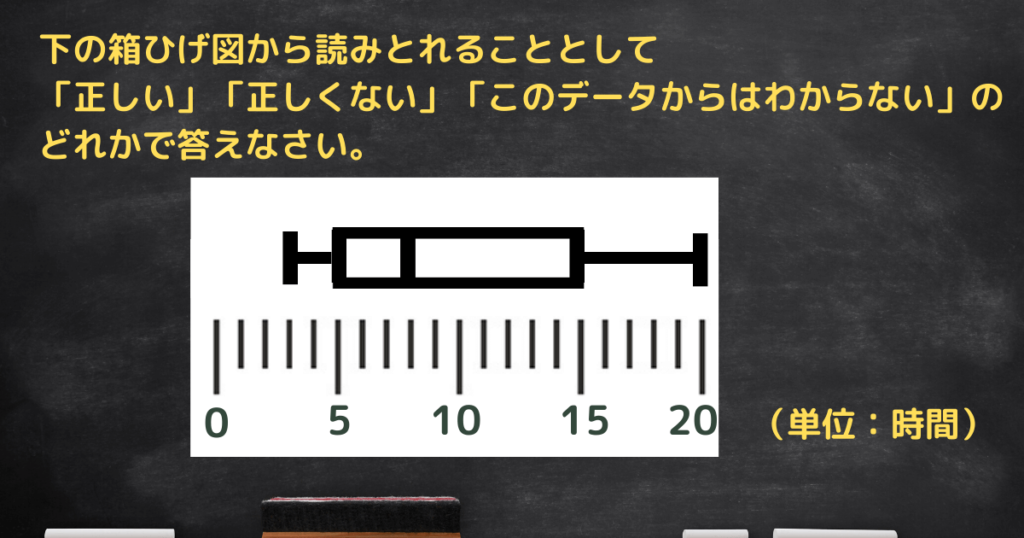
「正しい」「正しくない」「このデータではわからない」を判断する問題を5問出題します!
(タップで答えを確認できます)
(1)最大値は20時間である。
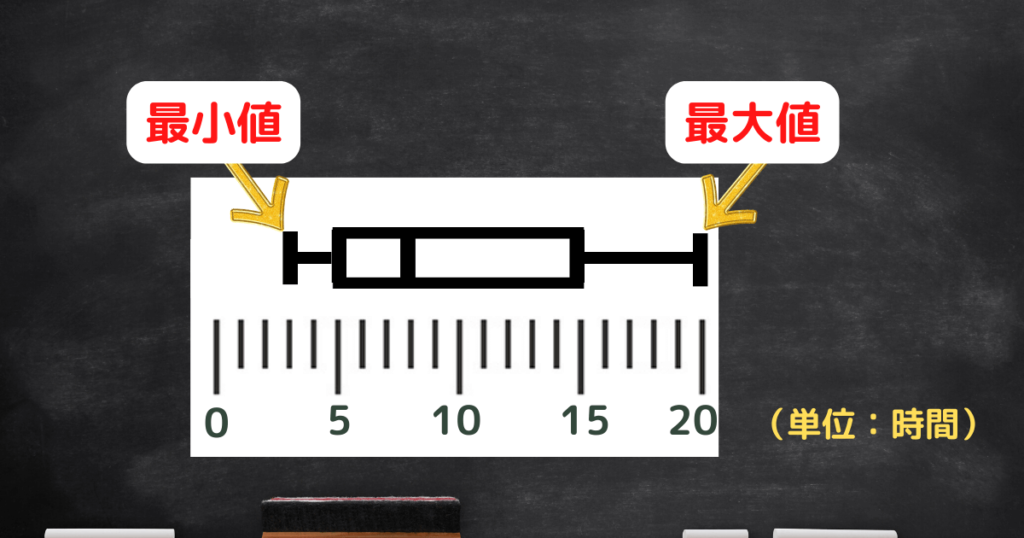
(1)最大値は20時間である。
⇒「正しい」
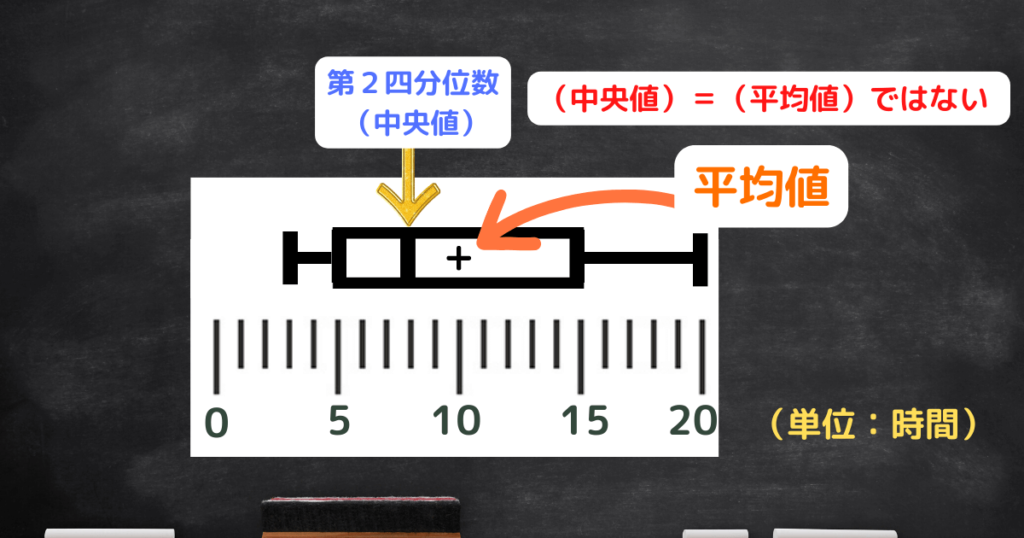
(2)平均値は8時間である。
 プロ講師エリ
プロ講師エリ「中央値」=「平均値」ではないことを押さえましょう!
「平均値」は「+」マークをつけて表すことがあります。
(2)平均値は8時間である。
⇒「このデータからはわからない」
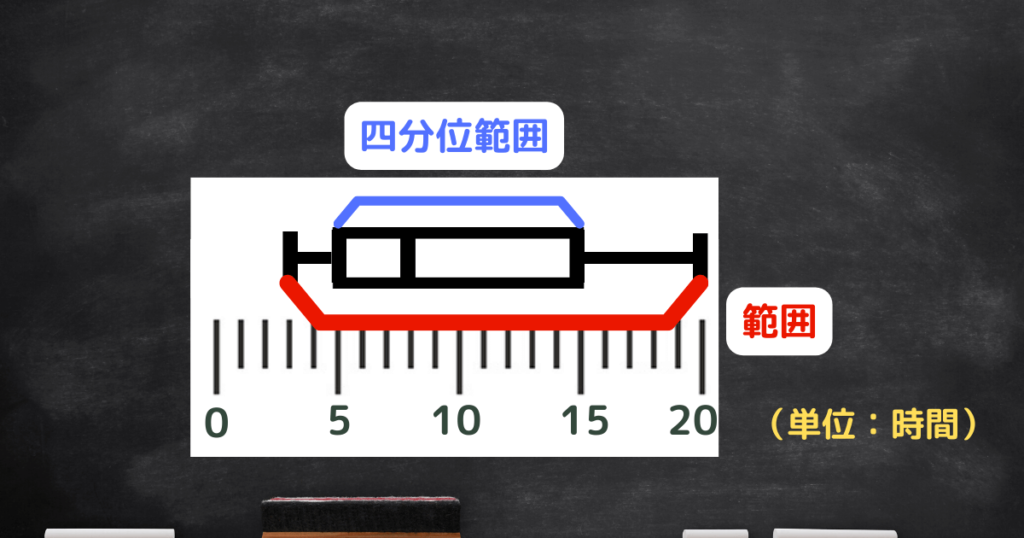
(3)四分位範囲は17時間である。
 保護者
保護者「四分位範囲」は
15ー5=10時間!
「範囲」と「四分位範囲」の違いに気をつけなきゃ。
(3)四分位範囲は17時間である。
⇒「正しくない」
(4)データの個数は10個である。

(4)データの個数は10個である。
⇒「このデータからはわからない」
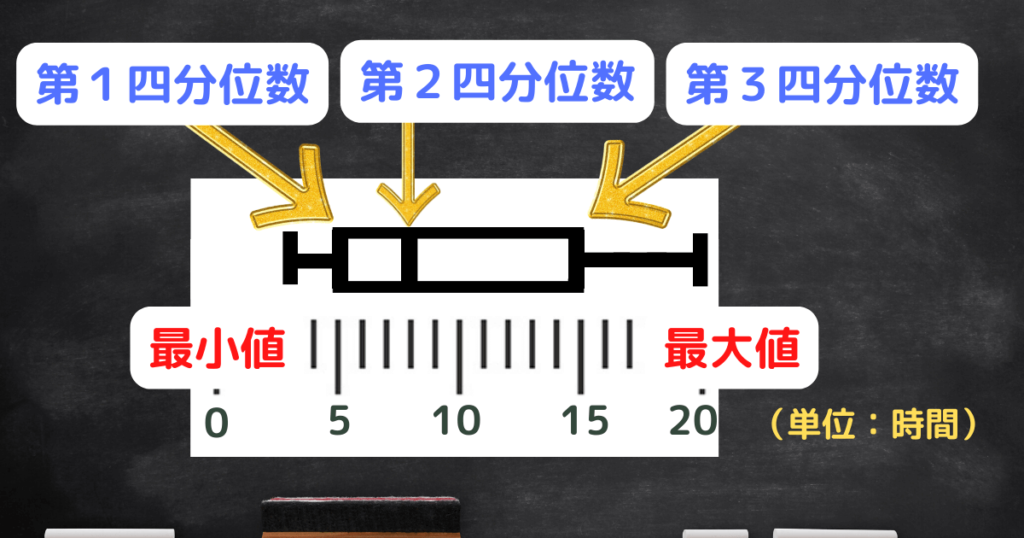
(5)データの25パーセントは、15時間以上である。
 プロ講師エリ
プロ講師エリ「四分位数」とは、データを小さい順に並べたとき4等分(25パーセントずつ)する3つのしきりです。
 保護者
保護者「第3四分位数」が15時間だから、15時間以上に「25パーセント」いることがわかるのね。
(5)データの25パーセントは、15時間以上である。
⇒「正しい」
コラム:「中央値」と「平均値」の違い

 保護者
保護者「中央値」と「平均値」の違いって何?
 プロ講師エリ
プロ講師エリ「中央値」の「真ん中」に対し、「平均値」はデータの凸凹を「ならす(平らにする)」という考え方です。
 保護者
保護者上の例題の「中央値」は8時間。
「平均値」は10時間。
あまり差がないような・・・
 プロ講師エリ
プロ講師エリ差がないとは言い切れません。
数値を変えてみます!
「最大値」を20⇒130に変えると・・・

 保護者
保護者「平均値」が大きく変わった!全く「真ん中」じゃないよ・・・
例題② 「箱ひげ図」と「ヒストグラム」
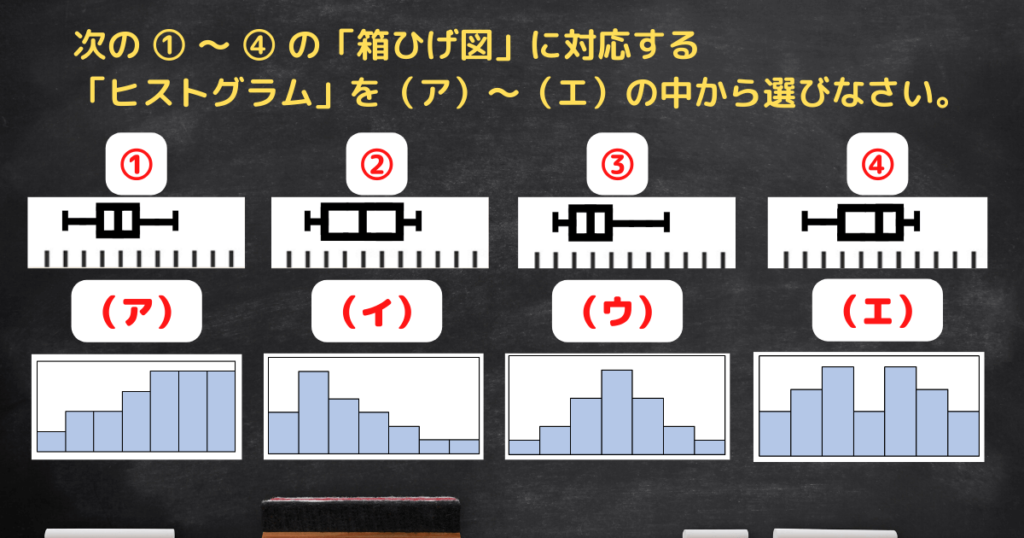
次は、中2で習う「箱ひげ図」と中1で習う「ヒストグラム」をあわせた出題です。
同じデータから作られた「箱ひげ図」と「ヒストグラム」の組み合わせを探しましょう。
ここをタップで答え合わせ!
(答え)
①(ウ)
②(エ)
③(イ)
④(ア)
 プロ講師エリ
プロ講師エリはじめは戸惑うかもしれません。
どこに注目すべきか「コツ」を教えます!
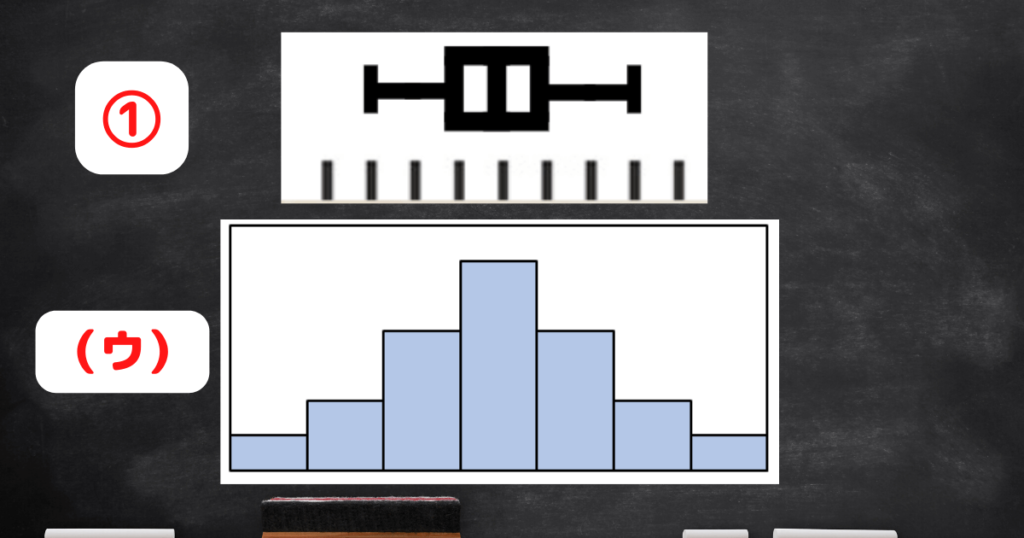
「箱ひげ図」の①と②、「ヒストグラム」の(ウ)と(エ)は左右対称です。
「箱ひげ図」①が「ヒストグラム」(ウ)と対応しています。
「箱ひげ図」の「箱(長方形部分)」に注目すると
②よりも①の「箱」の方が小さく、データが中央に集中していることがわかります。
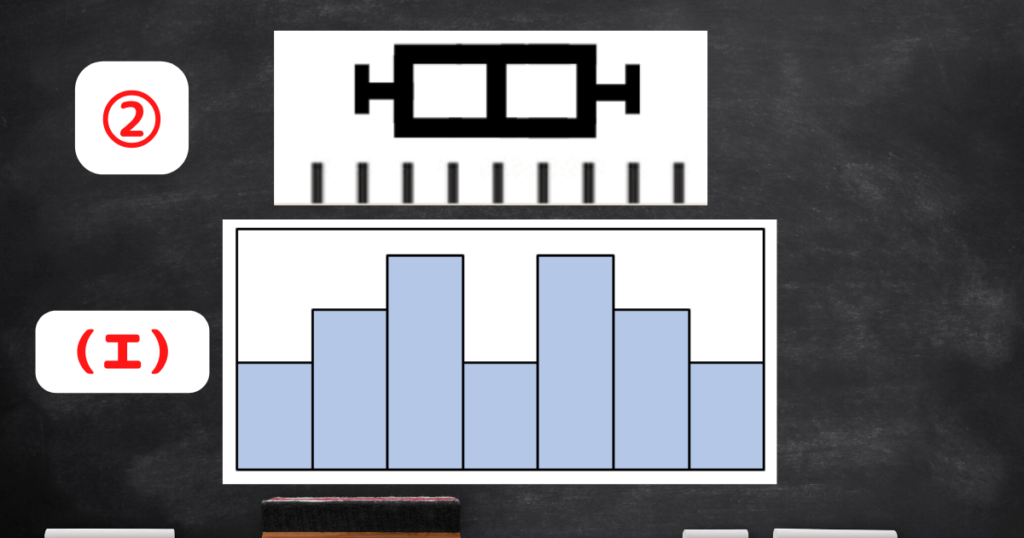
「箱ひげ図」②が「ヒストグラム」(エ)と対応しています。
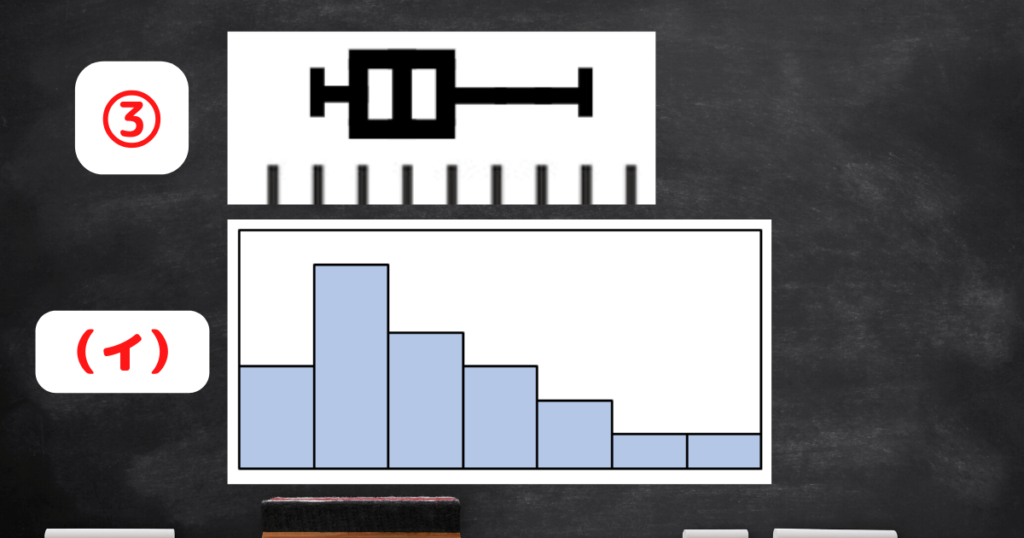
「箱ひげ図」③が「ヒストグラム」(イ)と対応しています。
 保護者
保護者「箱ひげ図」の「箱」が左に偏っているから、
「ヒストグラム」の「山」も左に偏っているものを選ぶのね!
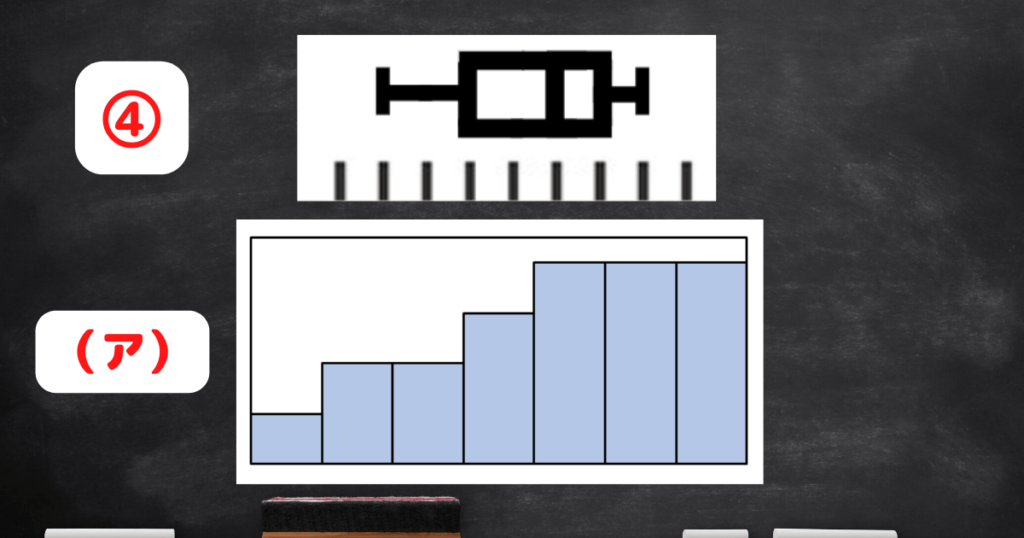
「箱ひげ図」④が「ヒストグラム」(ア)と対応しています。
どちらも右に偏っているのがわかります。
コラム:「箱ひげ図」と「ヒストグラム」の比較
「箱ひげ図」と「ヒストグラム」の違いを表にまとめました。
(ひと目でわかるとは、計算せずに見た目だけでわかるということです)
 プロ講師エリ
プロ講師エリそれぞれの特徴をおさえておきましょう!
例題③ 「中2データの活用」記述問題
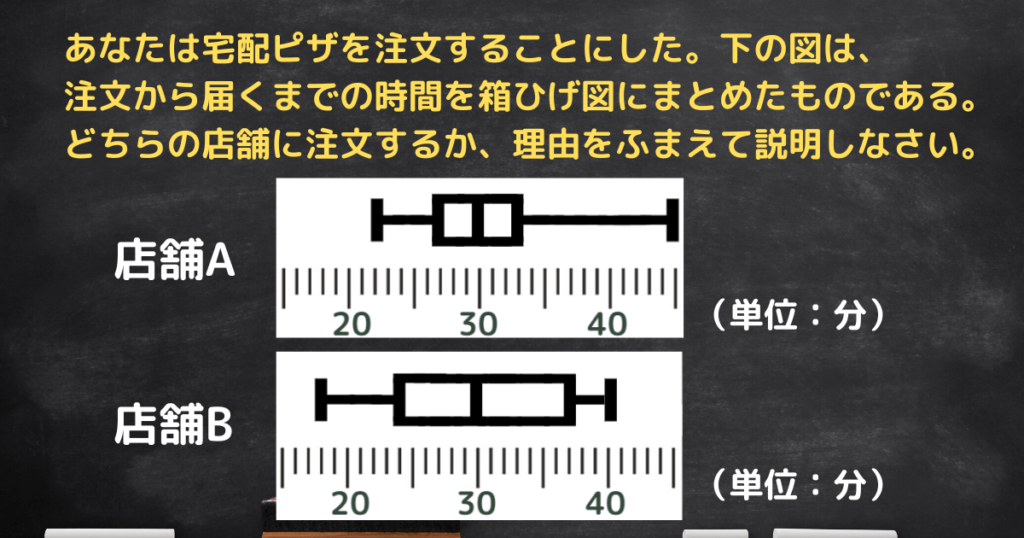
「資料を読みとった上で自分の考えを記述する」問題が出題されることがあります。
 プロ講師エリ
プロ講師エリ店舗A・店舗Bどちらを選んでも構いません!
(どのような理由で選ぶかが重要です)
(店舗Aに注文する)ここをタップで答え合わせ!
(答え)※例
店舗Aと店舗Bの中央値はどちらも等しい。
データの中央付近のほぼ50%(四分位範囲)を見ると、店舗Aの方が店舗Bよりも中央に集まっている(散らばりが小さい)ことがわかるので、店舗Aに注文する。
(店舗Bに注文する)ここをタップで答え合わせ!
(答え)※例
店舗Bの最小値が店舗Aの最小値よりも小さいので、店舗Bに注文する。
「箱ひげ図」からは、「最小値」「最大値」「四分位数」「中央値」「範囲」「データのちらばり」などの情報が読みとれます。
どれかの情報をもとに、自分の考えを述べましょう!
「中2データの活用」まとめの練習問題
練習問題①
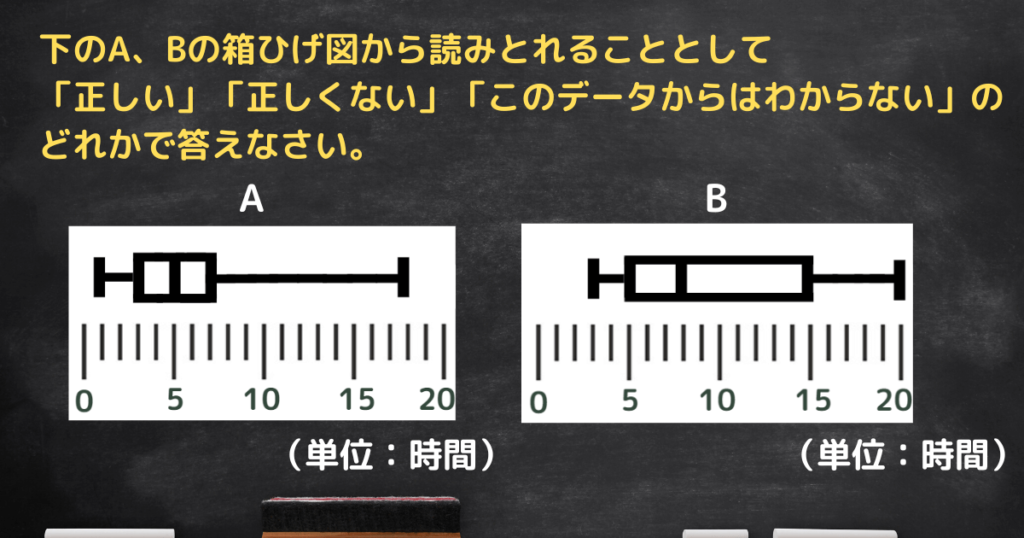
A、Bについて「正しい」「正しくない」「このデータからはわからない」を判断する問題を5問出題します!
(タップで答えを確認できます)
(1)Aの平均値は5時間である。
(答え)
「このデータからはわからない」
 プロ講師エリ
プロ講師エリ「中央値」は5時間です!
「平均値」は書かれていないのでわかりません。
(2)AとBの範囲は等しい。
(答え)
「正しい」
 保護者
保護者Aの「範囲」は
18ー1=17時間
Bの「範囲」は
20ー3=17時間
どちらも等しくなるね!
(3)Bのデータの個数は17個である。
(答え)
「このデータからはわからない」
(4)Bのデータの30パーセントは、15時間以上である。
(答え)
「正しくない」
 プロ講師エリ
プロ講師エリ「第3四分位数」が15時間なので、15時間以上といえるのは25パーセントです。
(5)AよりBの方がデータの散らばり具合が大きい。
(答え)
「正しい」
 保護者
保護者Aの「四分位範囲」は
7ー3=4時間
Bの「四分位範囲」は
15ー5=10時間
Bの方が「散らばりが大きい」とわかるね!
練習問題②
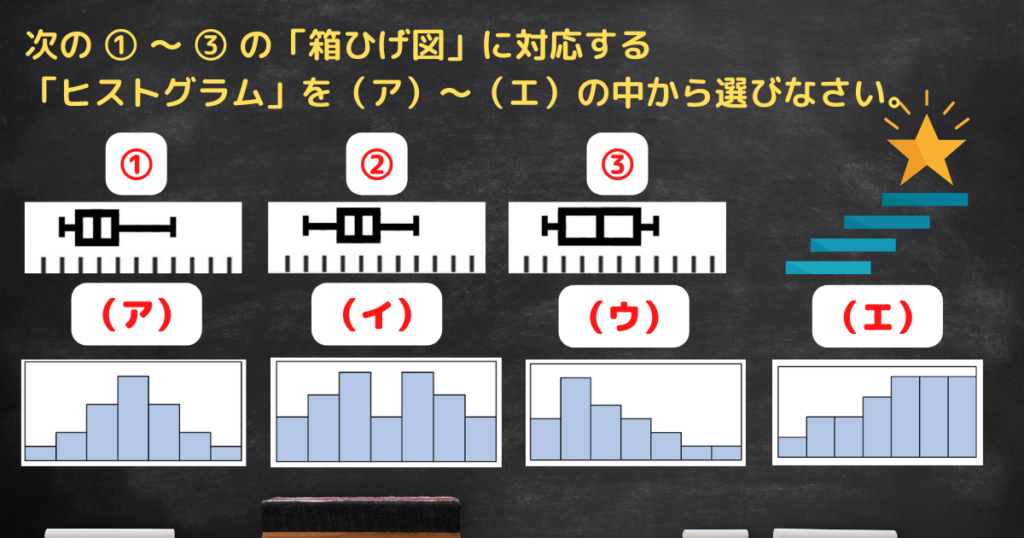
次は「箱ひげ図」と「ヒストグラム」の組み合わせを選ぶ問題です。
ここをタップで答え合わせ!
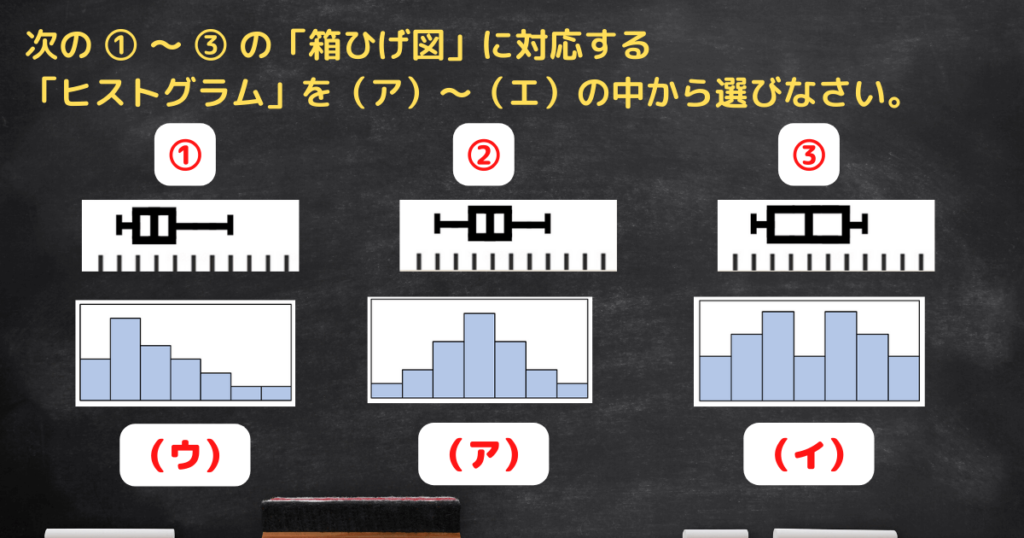
(答え)
①(ウ)
②(ア)
③(イ)
 プロ講師エリ
プロ講師エリ①は「左に偏っている」
②は左右対称で「中央に集中している」
③も左右対称で「②よりも散らばりが大きい」
これをもとに「ヒストグラム」を選びましょう!
練習問題③
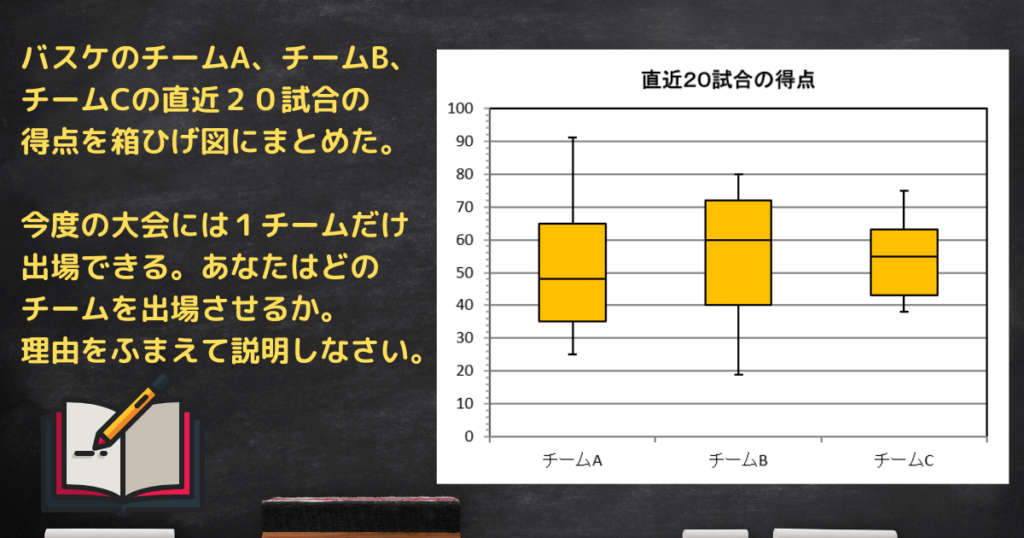
最後の問題は、データを比較して記述しましょう。
チームA、チームB、チームCのどれを選んでも構いません。
(チームAを出場させる)ここをタップで答え合わせ!
(答え)※例
得点の最大値が最も大きいので、チームAを選ぶ。
(チームBを出場させる)ここをタップで答え合わせ!
(答え)※例
得点が60点以上の試合が最も多いので、チームBを選ぶ。
(チームBは試合の25パーセントが72点以上得点している)
(チームCを出場させる)ここをタップで答え合わせ!
(答え)※例
最も四分位範囲(データの散らばり)が小さいので、得点が中央に集まって安定しているチームCを選ぶ。
「中2データの活用」まとめ

この記事では、「四分位数」や「箱ひげ図」の考え方を用いて【中2データの活用】応用問題を解いていきました。
【データの活用】で、中2の数学は終わりです。
この記事で学ぶこと
・「箱ひげ図」の情報が「正しい」か「正しくない」か「わからない」かを選ぶ
⇒例題にジャンプ!
・対応する「箱ひげ図」と「ヒストグラム」を選ぶ
⇒例題にジャンプ!
・「箱ひげ図」を比較して記述する
⇒例題にジャンプ!
記事内の問題は無料ダウンロードできます
 プロ講師エリ
プロ講師エリ中3の最初は「計算分野」を習います!